卷积核
卷积核本质上是一个非常小的矩阵,最常用的是 3×3 矩阵。主要是利用核与图像之间进行卷积运算来实现图像处理,能做出模糊、锐化、凹凸、边缘检测等效果。
神经网络中卷积核的维度和对(3*3,2)的理解(我的理解)
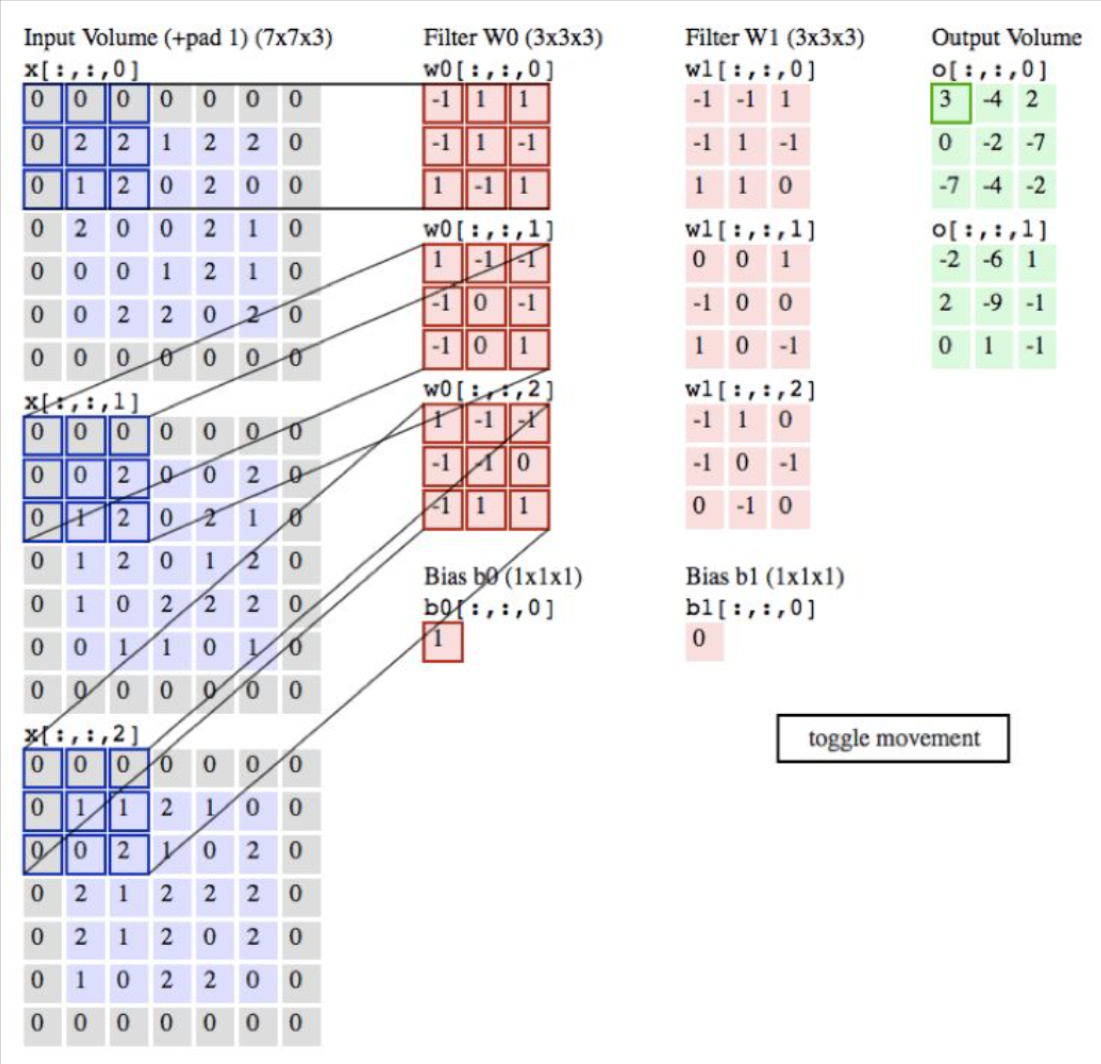
图中输入数据为蓝色部分是一张5*5*3的三维图片,padding=1,变为7*7*3。
图中权重数据体为红色部分是两个3*3*3的卷积核,因为输入的数据为3维所以每个卷积核都是3维的,又因为要将输入数据变为3*3*2所以需要两个,在神经网络中可以写成(3*3,2)。
正式一点:对于RGB图像,图像为3维,若要提取2个特征,可以设置2个3维卷积核进行特征提取,提取结果为2通道的feature map,2个通道互相独立,代表着不同卷积核提取的不同特征。
卷积层演示:下面是一个卷积层的运行演示。因为3D数据难以可视化,所以所有的数据(输入数据体是蓝色,权重数据体是红色,输出数据体是绿色)都采取将深度切片按照列的方式排列展现。输入数据体的尺寸是W1=5,H1=5,D1=3,卷积层参数K=2,F=3,S=2,P=1。
K:卷积核个数
F:卷积核大小
S:步长
P:填充数
就是说,有2个滤波器,滤波器的尺寸是3⋅3,它们的步长是2。
因此,输出数据体的空间尺寸是(5-3+2)/2+1=3。
注意输入数据体使用了零填充P=1,所以输入数据体外边缘一圈都是0。
下面的例子在绿色的输出激活数据上循环演示,展示了其中每个元素都是先通过蓝色的输入数据和红色的滤波器逐元素相乘,然后求其总和,最后加上偏差得来。
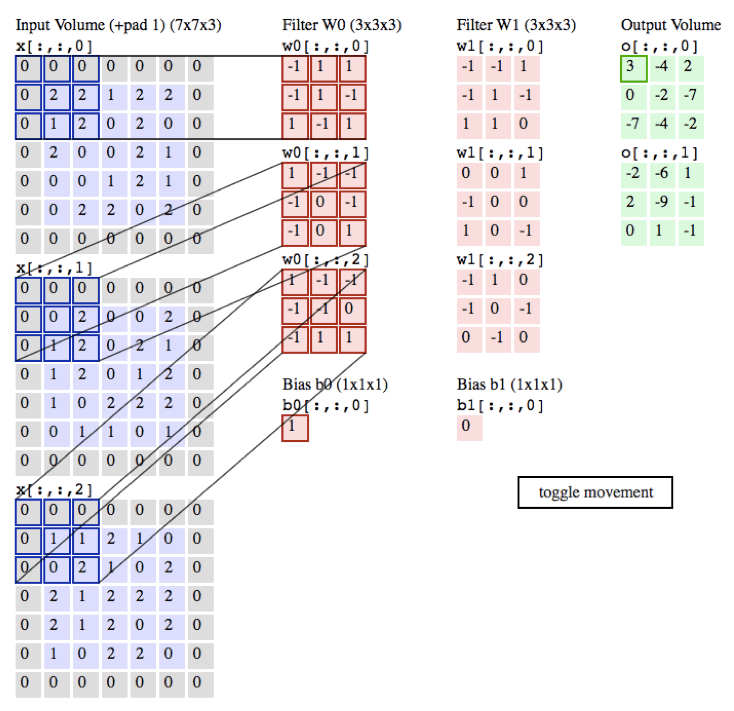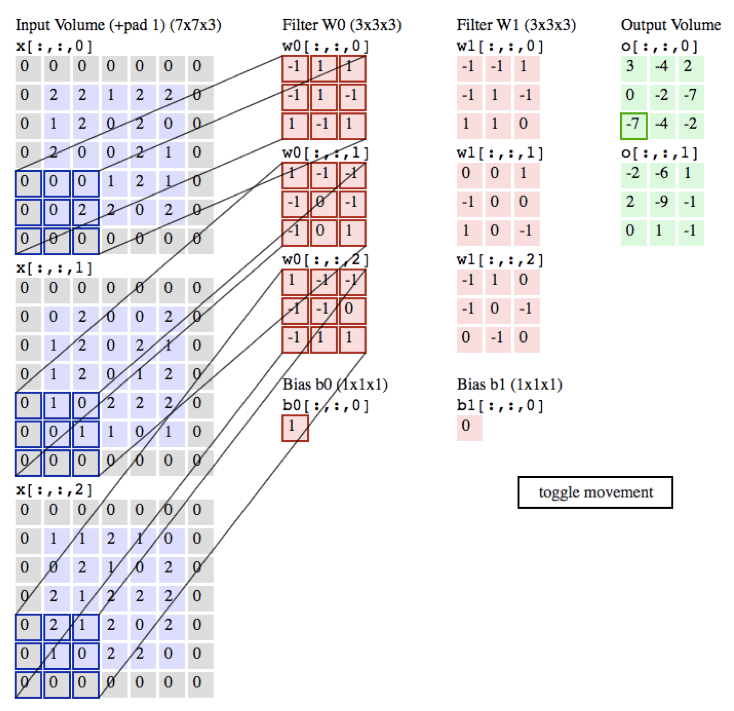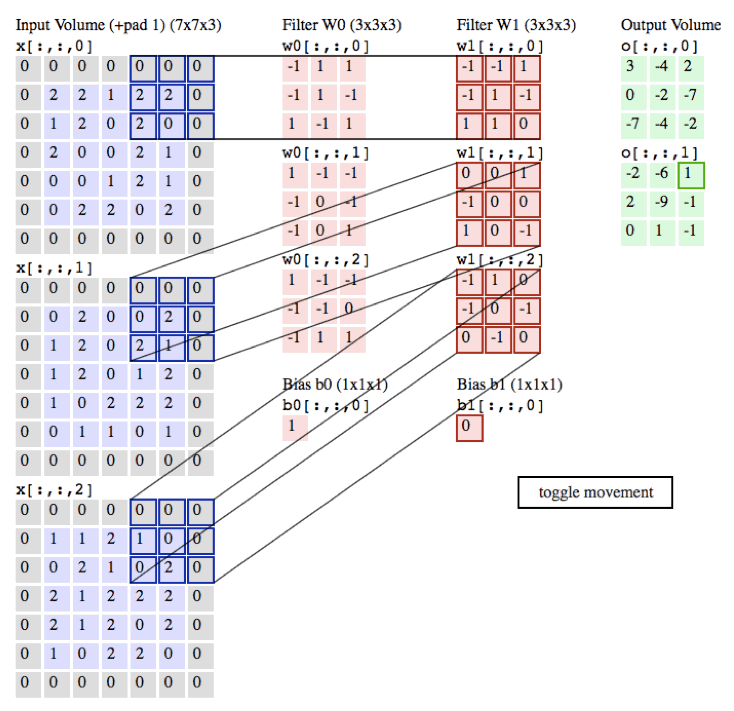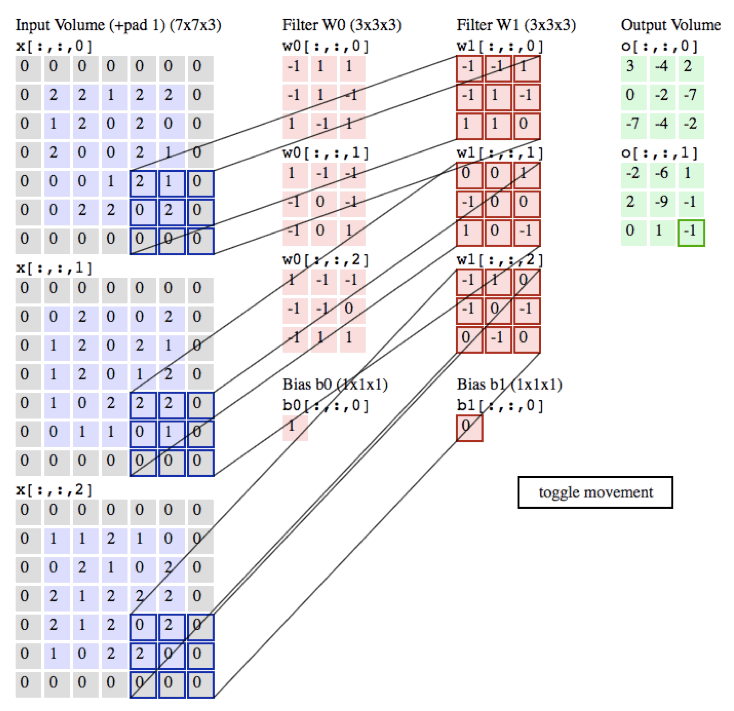
参数数量的计算:
- 概念图
进行卷积处理的卷积通道数默认和输入图像的通道数相等。
比如输入图像维度为256,进行特征提取的卷积核也默认是256维。
若设定输出64个特征,那么就一共有64个256维的卷积核用来提取特征,即提取特征的输出通道数为64,输出64个feature map。
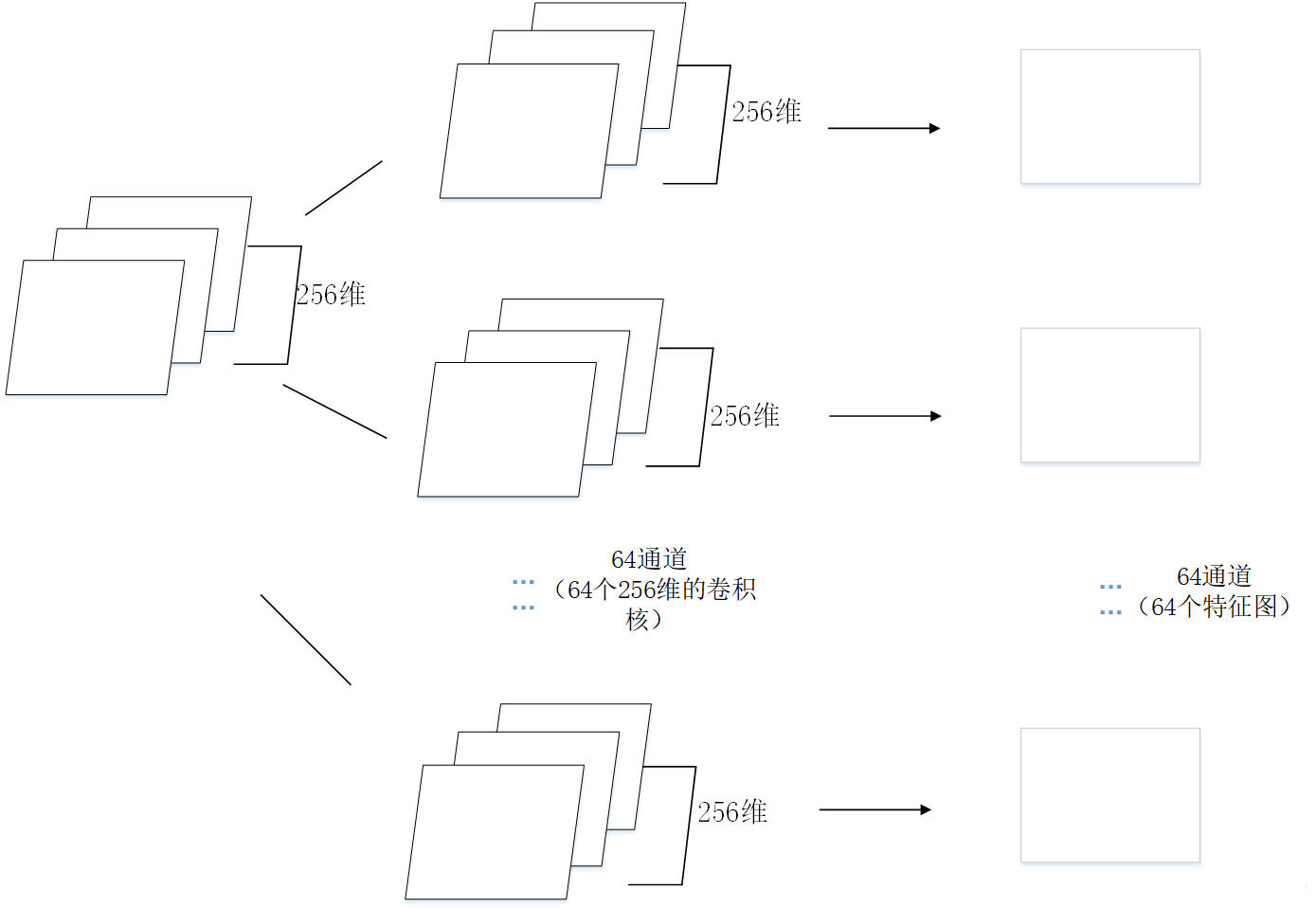
- 运算过程
左侧:全连接层就是两个3*3*256的卷积,参数数目:3*3*256*256*2 = 1179648,差了16.94倍
右侧:第一个1*1的卷积把256维channel降到64维,然后在最后通过1*1卷积恢复,参数数目:1*1*256*64 + 3*3*64*64 + 1*1*64*256 = 69632
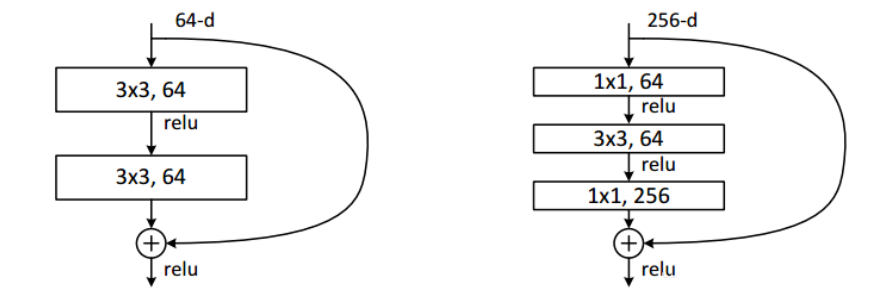
小卷积核
一般指的都是大小为3*3的卷积核,可以有多个通道数
eg:一个(3*3,64)的卷积核就是指长×宽为3×3,64个
- 一个5*5的卷积核可以用两个3*3的代替
例如:输入的特征图为64*64的,
- 用5*5的卷积核进行卷积,步长设为1,输出的特征图为$ceil((64-5+1)/1)=60$,即为60*60的大小
- 用两个3*3的分别进行卷积,步长也设为1,
第一步:$ceil((64-3+1)/1)=62$
第二步:$ceil((62-3+1)/1)=60$
结果也为60*60
由上可见,两种结果是相同的,说明一个5*5的卷积核完全可以用两个3*3的代替
相似的,一个7*7的卷积核可以用三个3*3的代替;一个9*9的卷积核可以用四个3*3的代替
小卷积核优点
- 参数量少
就拿上边的那个例子说,两个3*3的卷积核参数量为3*3*2=18,一个5×5的卷积核参数量为5*5=25,可见小卷积核参数量要小(此处都是用1通道,若加入多通道,参数量更是成倍的增加,小卷积核参数量少的优势就更加的明显)
- 小卷积核堆叠使用,可以使得模型的非线性表达能力更好
神经网络里边,每一层卷积后都要跟一个激活层(要注意,写神经网络时,激活层可不能少),卷积层多了,激活层也变多,非线性表达能力变好。
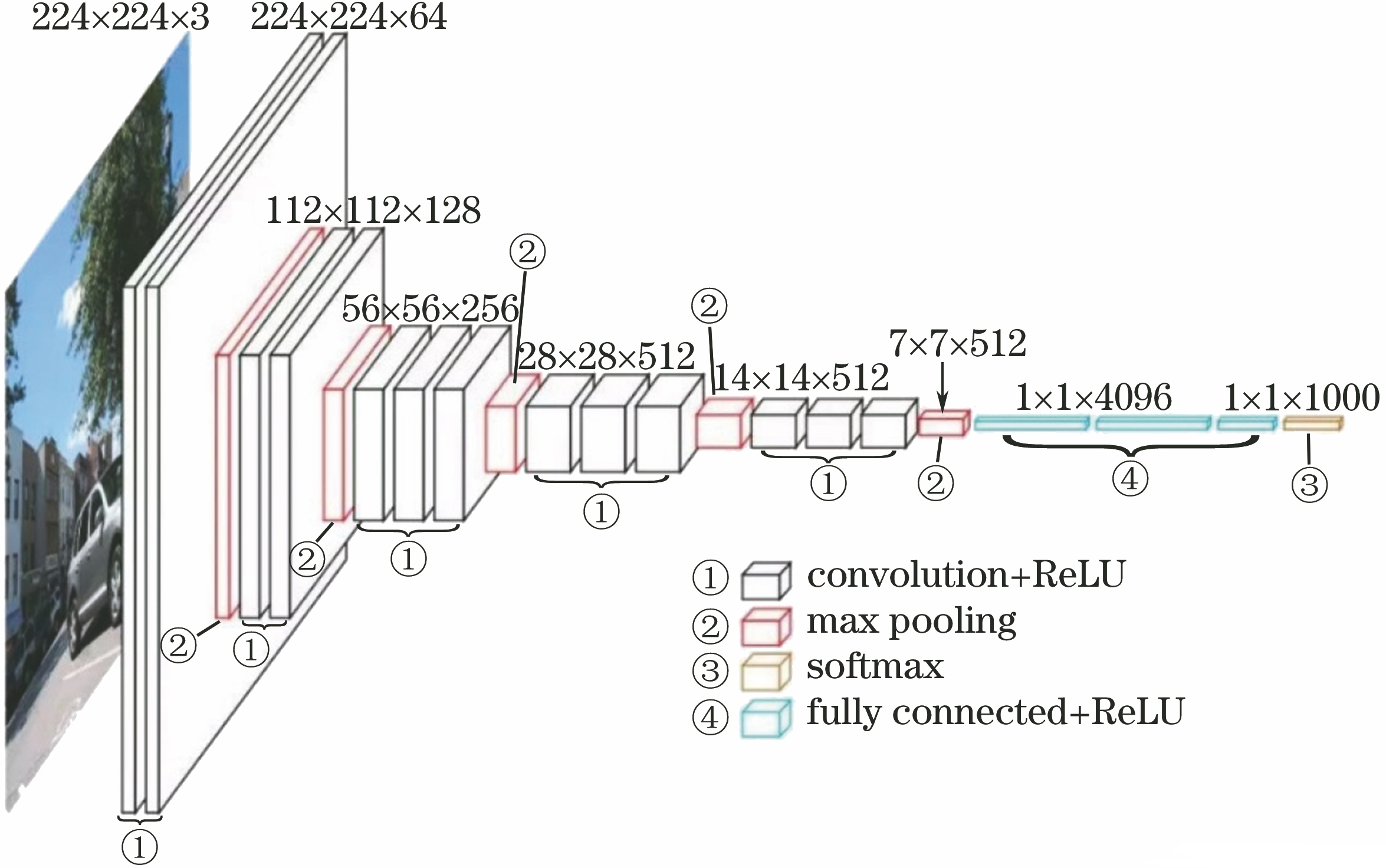
明确的标出了,卷积层和全连接层后边都要加一个激活函数。
- 小卷积核堆叠使用,还能使模型的计算量减少
此处的计算量一般都是指乘法运算,加法就不算在内了
计算量计算的公式:
$$ 计算量=(卷积核大小c\times w\times h)\times(输出特征图大小c\times w\times h) $$
很容易想到,每做一次卷积进行的乘法操作,就是卷积核每个位置和对应位置相乘,那一次卷积操作的乘法运算量不就是卷积核的大小么,最后变成的不就是输出特征图的一个值吗;那要做多少次卷积,不就是特征图有多大,就做多少次么,所以能得到这个结果。
还拿上边的那个例子来说吧,
- 一个5*5卷积的运算量为
$(5\times 5\times 1)\times(60\times 60\times 1)=90000$ - 两个3*3卷积的运算量为
$(3\times 3\times 1)\times (62\times 62\times 1)+(3\times 3\times 1)\times (60\times 60 \times 1)=34596+32400=66996$
可以看出小卷积核的运算量是较少的
- 小卷积核堆叠使用可以达到和大卷积核一样的探测面积,还更能提取到有用特征,不会丢失重要特征。
多个小卷积核完全可以替代一个大卷积核,而且输出特征图大小还可保持不变,多次卷积又代表着多次提取特征,还能更好的提取有用特征。
确实看不懂
:)(erha) 学 哈哈哈哈哈