深度学习中Dropout原理解析
1. Dropout简介
1.1 Dropout出现的原因
在机器学习的模型中,如果模型的参数太多,而训练样本又太少,训练出来的模型很容易产生过拟合的现象。
在训练神经网络的时候经常会遇到过拟合的问题,过拟合具体表现在:
- 模型在训练数据上损失函数较小,预测准确率较高;
- 但是在测试数据上损失函数比较大,预测准确率较低。
过拟合是很多机器学习的通病。
如果模型过拟合,那么得到的模型几乎不能用。
为了解决过拟合问题,一般会采用模型集成的方法,即训练多个模型进行组合。
此时,训练模型费时就成为一个很大的问题,不仅训练多个模型费时,测试多个模型也是很费时。
综上所述,训练深度神经网络的时候,总是会遇到两大缺点:
- 容易过拟合
- 费时
Dropout可以比较有效的缓解过拟合的发生,在一定程度上达到正则化的效果。
1.2 什么是Dropout
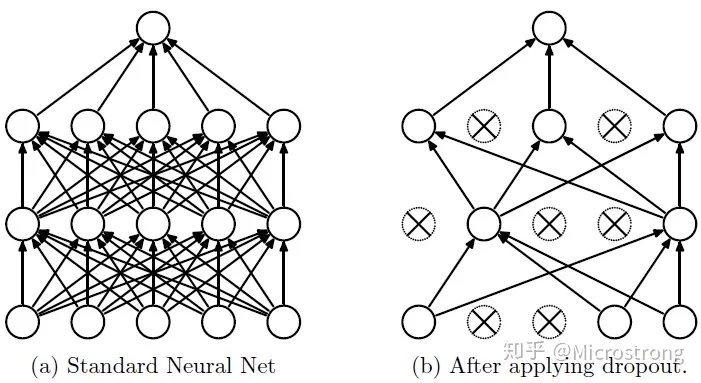
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中,通过忽略一半的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。
Dropout说的简单一点就是:我们在前向传播的时候,让某个神经元的激活值以一定的概率p停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征
2. Dropout工作流程及使用
2.1 Dropout具体工作流程
假设我们要训练这样一个神经网络
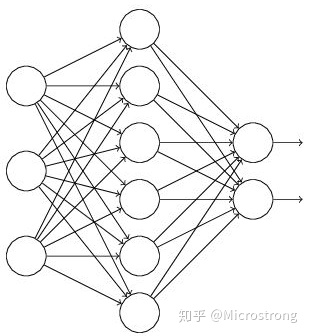
输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。
使用Dropout之后,过程变成如下:
- 首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(图3中虚线为部分临时被删除的神经元)
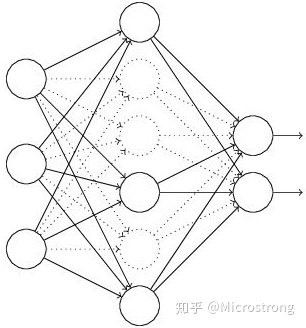
- 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
然后继续重复这一过程:
- 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
- 对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数$(w,b)$ (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
不断重复这一过程。
2.2 Dropout在神经网络中的使用
Dropout代码层面的一些公式推导及代码实现思路。
- 在训练模型阶段
无可避免的,在训练网络的每个单元都要添加一道概率流程。
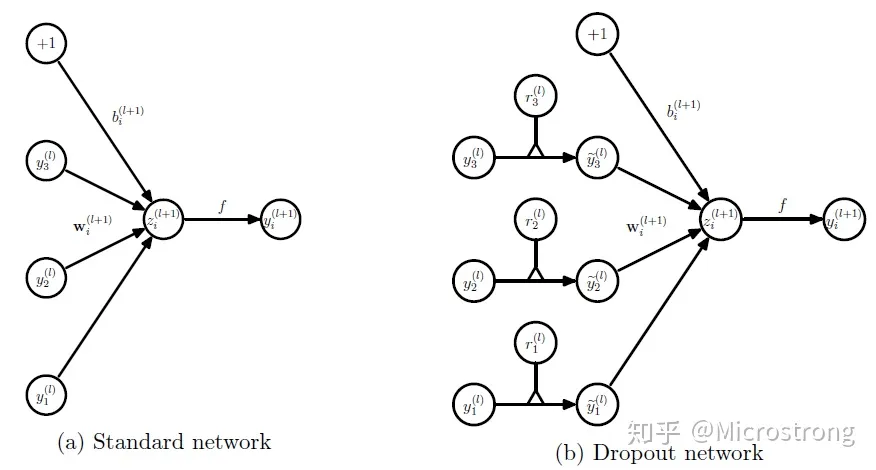
对应的公式变化如下:
没有Dropout的网络计算公式:
$$ \begin{aligned} z_i^{(l+1)}&=W_i^{(l+1)}y^l+b_i^{(l+1)}\\ y_i^{(l+1)}&=f(z_i^{(l+1)}) \end{aligned} $$
采用Dropout的网络计算公式:
$$ \begin{aligned} r_j^{(l)} & \sim Bernoulli(p)\\ \tilde{y}^{(l)}&=r^{(l)}*y^{(y)} \\ z_i^{(l+1)} &= w_i^{(l+1)}\tilde{y}^l+b_i(l+1)\\ y_i^{(l+1)} &= f(z_i^{(l+1)}) \end{aligned} $$
上面公式中Bernoulli函数是为了生成概率r向量,也就是随机生成一个0、1的向量。
代码层面实现让某个神经元以概率p停止工作,其实就是让它的激活函数值以概率p变为0。
比如我们某一层网络神经元的个数为1000个,其激活函数输出值为$y1、y2、y3、......、y1000$,我们dropout比率选择0.4,那么这一层神经元经过dropout后,1000个神经元中会有大约400个的值被置为0。
注意:经过上面屏蔽掉某些神经元,使其激活值为0以后,我们还需要对向量$y1……y1000$进行缩放,也就是乘以1/(1-p)。如果你在训练的时候,经过置0后,没有对$y1……y1000$进行缩放(rescale),那么在测试的时候,就需要对权重进行缩放,操作如下。
- 在测试模型阶段
预测模型的时候,每一个神经单元的权重参数要乘以概率p。
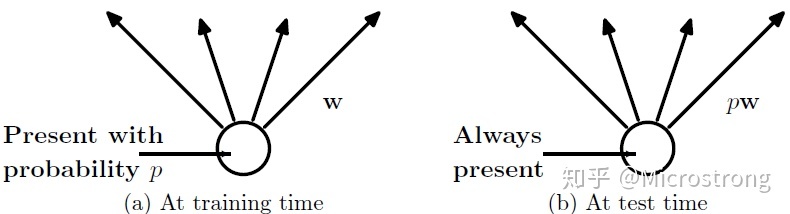
测试阶段Dropout公式:
$$ w^{(l)}_{test}=pW^{(l)} $$
3. 为什么说Dropout可以解决过拟合?
(1)取平均的作用: 先回到标准的模型即没有dropout,我们用相同的训练数据去训练5个不同的神经网络,一般会得到5个不同的结果,此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9,其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络,随机删掉一半隐藏神经元导致网络结构已经不同,整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合,一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
(2)减少神经元之间复杂的共适应关系: 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测,它不应该对一些特定的线索片段太过敏感,即使丢失特定的线索,它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像$L1,L2$正则,减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
(3)Dropout类似于性别在生物进化中的角色:物种为了生存往往会倾向于适应这种环境,环境突变则会导致物种难以做出及时反应,性别的出现可以繁衍出适应新环境的变种,有效的阻止过拟合,即避免环境改变时物种可能面临的灭绝。
思考
思考:Dropout为什么需要进行缩放呢?
因为我们训练的时候会随机的丢弃一些神经元,但是预测的时候就没办法随机丢弃了。如果丢弃一些神经元,这会带来结果不稳定的问题,也就是给定一个测试数据,有时候输出a有时候输出b,结果不稳定,这是实际系统不能接受的,用户可能认为模型预测不准。那么一种”补偿“的方案就是每个神经元的权重都乘以一个p,这样在“总体上”使得测试数据和训练数据是大致一样的。比如一个神经元的输出是x,那么在训练的时候它有p的概率参与训练,(1-p)的概率丢弃,那么它输出的期望是$px+(1-p)0=px$。因此测试的时候把这个神经元的权重乘以p可以得到同样的期望。
总结
当前Dropout被大量利用于全连接网络,而且一般认为设置为0.5或者0.3,而在卷积网络隐藏层中由于卷积自身的稀疏化以及稀疏化的ReLu函数的大量使用等原因,Dropout策略在卷积网络隐藏层中使用较少。总体而言,Dropout是一个超参,需要根据具体的网络、具体的应用领域进行尝试。