ResNet网络

ResNet网络

ResNet的亮点

• 超深的网络结构（超过1000层）
• 提出residual（残差结构）模块。
• 使用Batch Normalization 加速训练（丢弃dropout）。

为什么采用residual?

在ResNet提出之前，所有的神经网络都是通过卷积层和池化层的叠加组成的。

人们认为卷积层和池化层的层数越多，获取到的图片特征信息越全，学习效果也就越好。

但是在实际的试验中发现，随着卷积层和池化层的叠加，不但没有出现学习效果越来越好的情况，反而两种问题：

1. 梯度消失和梯度爆炸
   梯度消失：若每一层的误差梯度小于1，反向传播时，网络越深，梯度越趋近于0
   梯度爆炸：若每一层的误差梯度大于1，反向传播时，网络越深，梯度越来越大

2. 退化问题
   随着层数的增加，预测效果反而越来越差。如下图所示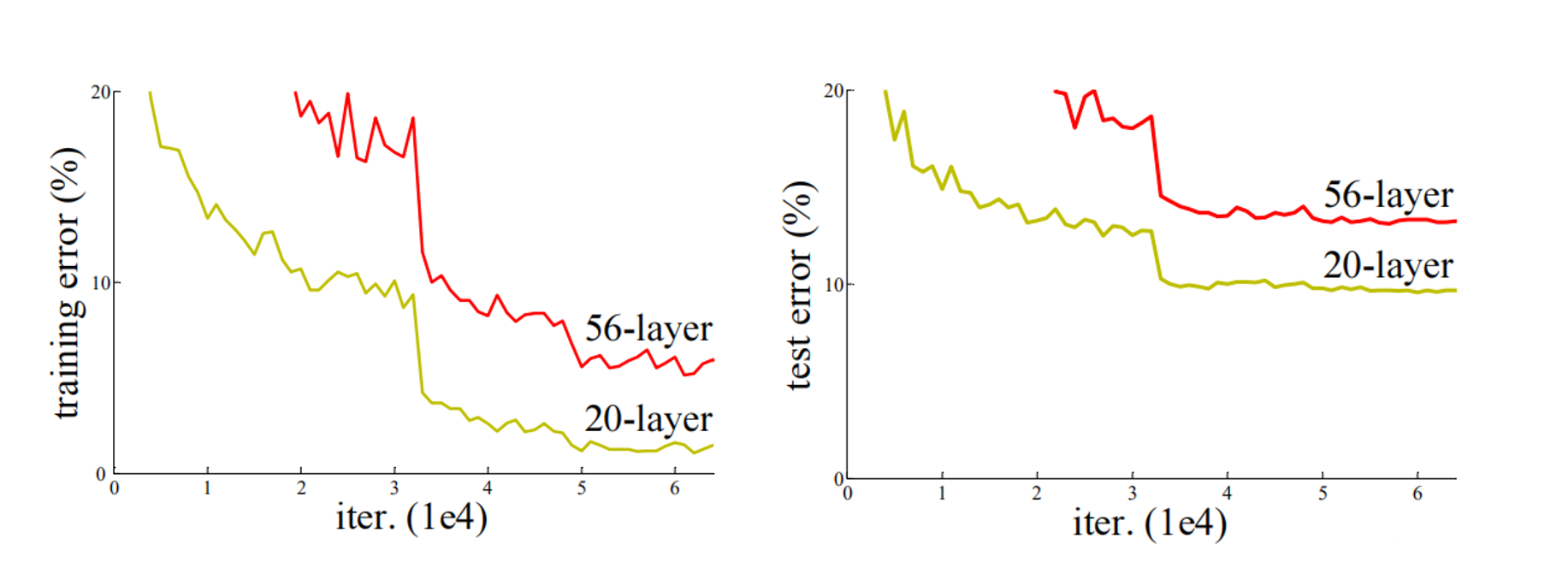
   

   • 为了解决梯度消失或梯度爆炸问题，ResNet论文提出通过数据的预处理以及在网络中使用 BN（Batch Normalization)层来解决。
   • 为了解决深层网络中的退化问题，可以人为地让神经网络某些层跳过下一层神经元的连接，隔层相连，弱化每层之间的强联系。这种神经网络被称为 残差网络 (ResNets)。ResNet论文提出了 residual结构（残差结构）来减轻退化问题，下图是使用residual结构的卷积网络，可以看到随着网络的不断加深，效果并没有变差，而是变的更好了。（虚线是train error，实线是test error）

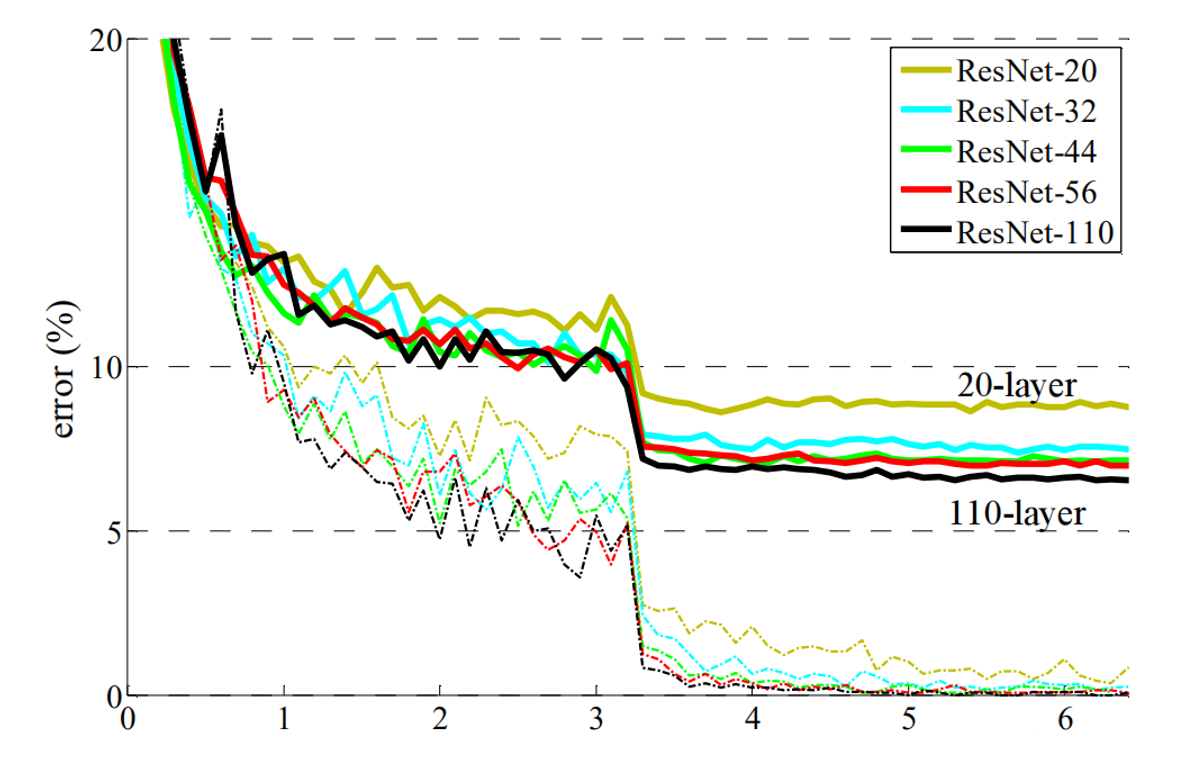
residual结构

residual的计算方式

residual结构使用了一种shortcut的连接方式，也可理解为捷径。让特征矩阵隔层相加，注意F(X)和X形状要相同，所谓相加是特征矩阵相同位置上的数字进行相加。

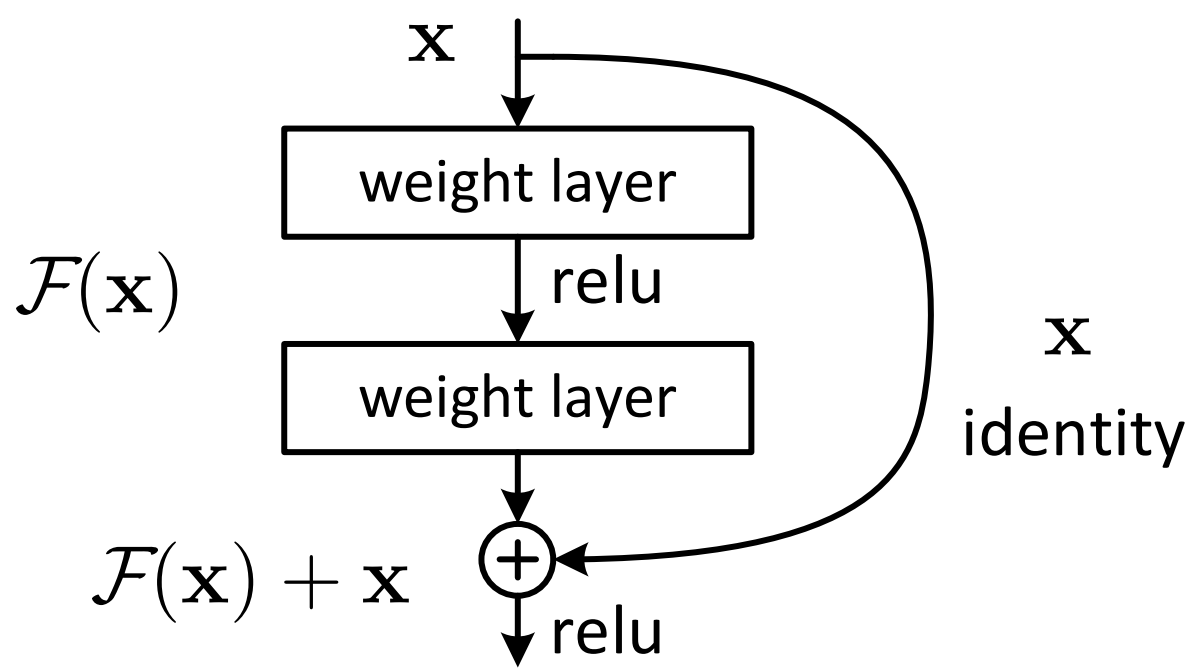
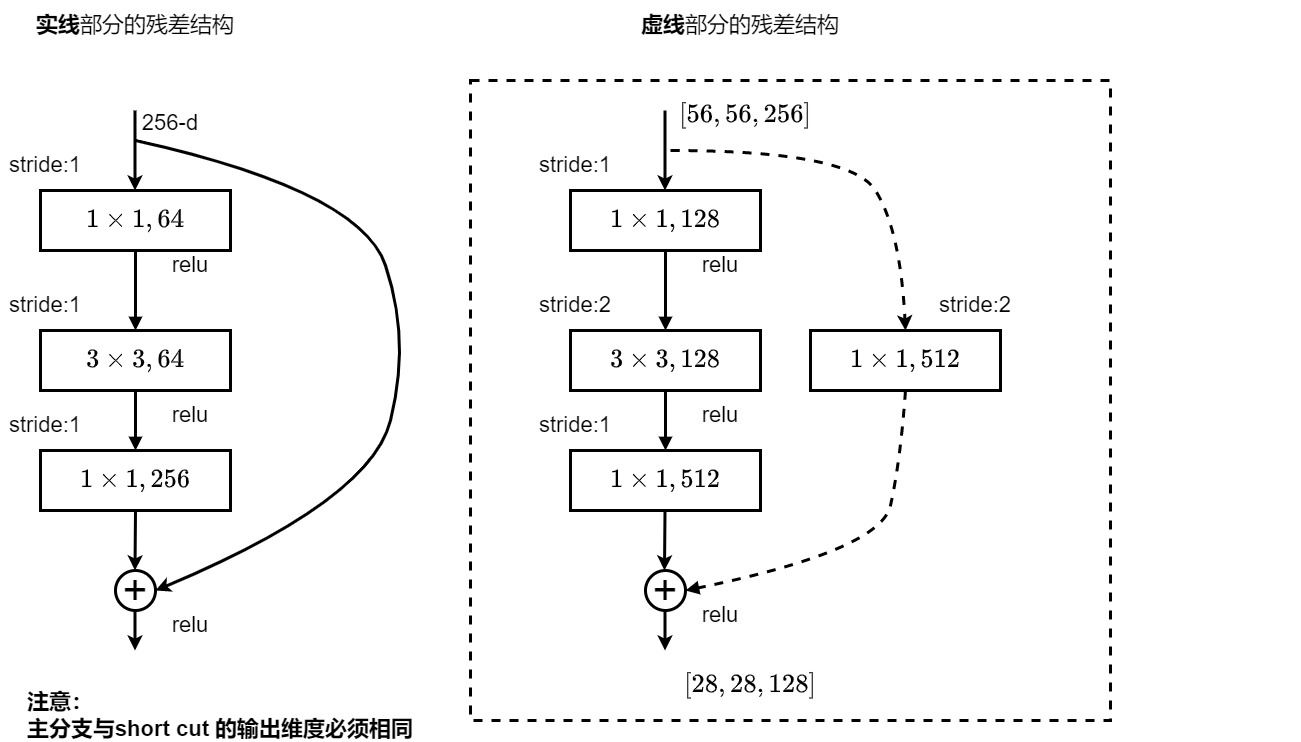
ResNet中两种不同的residual

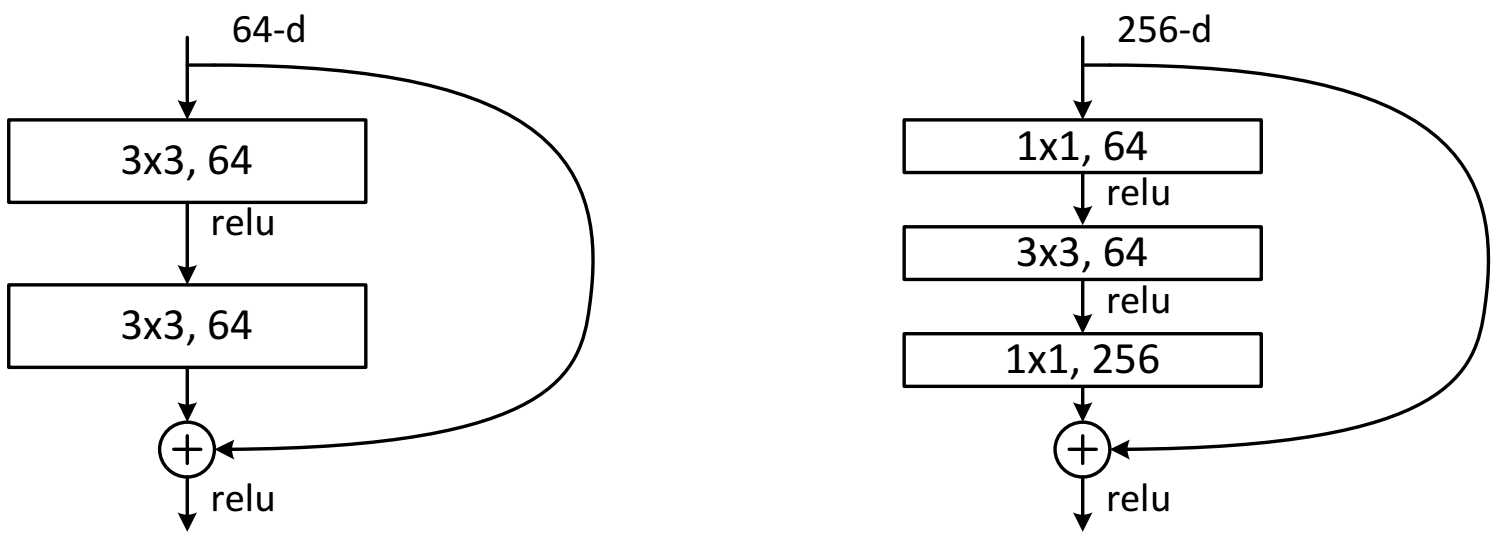
• 左侧残差结构称为 BasicBlock
• 右侧残差结构称为 Bottleneck

1. 其中第一层的1*1的卷积核的作用是对特征矩阵进行降维操作，将特征矩阵的深度由256降为64;
   第三层的1* 1的卷积核是对特征矩阵进行升维操作，将特征矩阵的深度由64升成256。
   降低特征矩阵的深度主要是为了减少参数的个数。

   如果采用BasicBlock,参数的个数应该是：256*256*3*3*2=1179648

   采用Bottleneck，参数的个数是：1*1*256*64+3*3*64*64+1*1*256*64=69632

2. 先降后升为了主分支上输出的特征矩阵和捷径分支上输出的特征矩阵形状相同，以便进行加法操作。

注：CNN参数个数 = 卷积核尺寸×卷积核深度 × 卷积核组数 = 卷积核尺寸 × 输入特征矩阵深度 × 输出特征矩阵深度

注意：搭建深层次网络时，采用三层的残差结构。

降维时的 short cut

观察下图的 ResNet18层网络，可以发现有些残差块的 short cut 是实线的，而有些则是虚线的。

这些虚线的 short cut 上通过1*1的卷积核进行了维度处理（特征矩阵在长宽方向降采样，深度方向调整成下一层残差结构所需要的channel）。

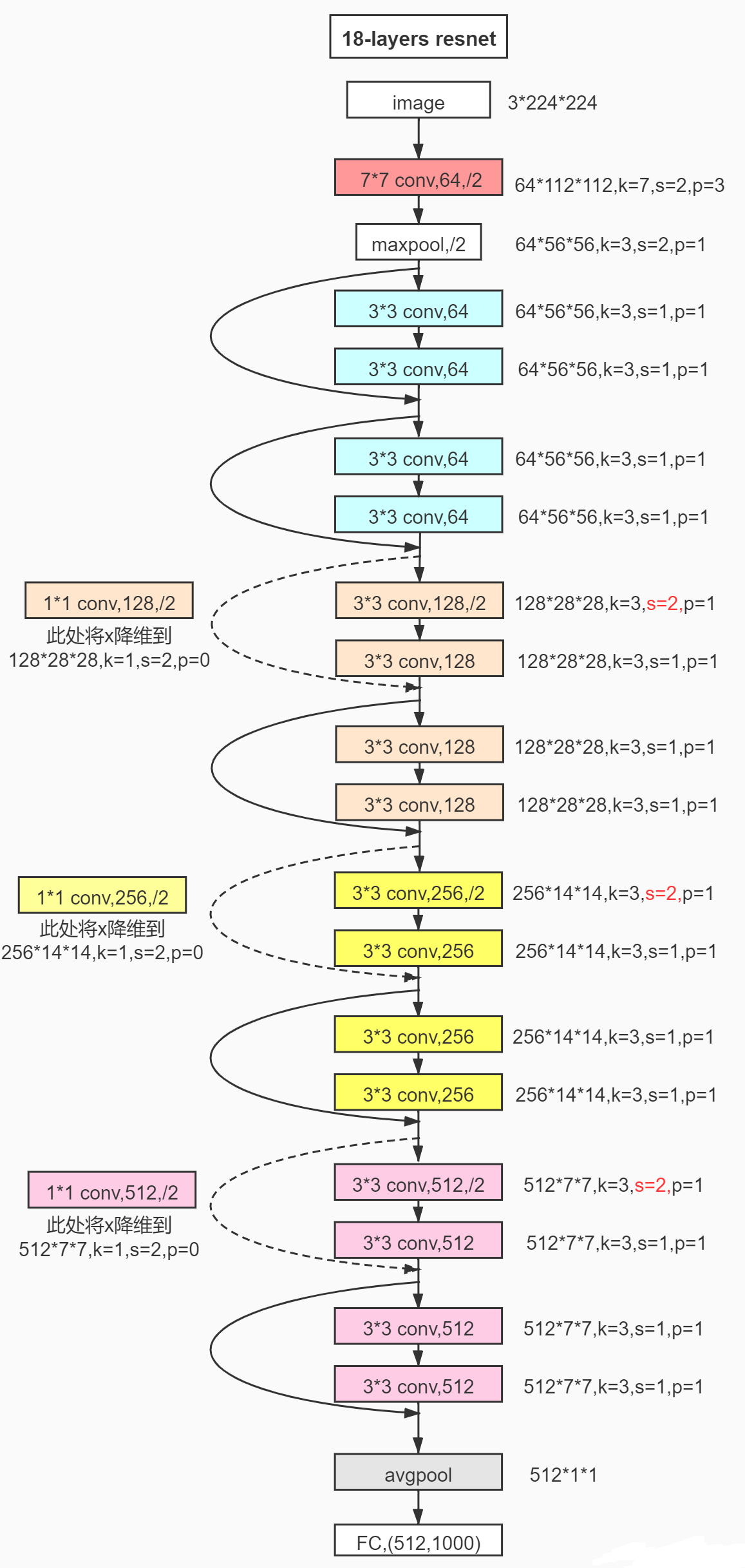
下图是原论文给出的不同深度的ResNet网络结构配置，注意表中的残差结构给出了主分支上卷积核的大小与卷积核个数，表中 残差块*N 表示将该残差结构重复N次。

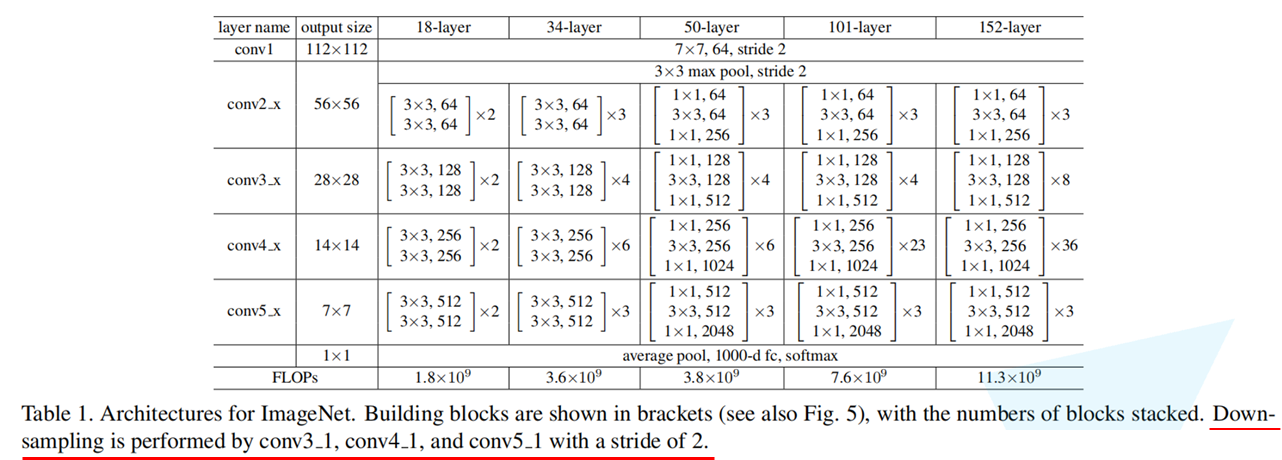
原文的标注中已说明，conv3_x, conv4_x, conv5_x所对应的一系列残差结构的第一层残差结构都是虚线残差结构。因为这一系列残差结构的第一层都有调整输入特征矩阵shape的使命（将特征矩阵的高和宽缩减为原来的一半，将深度channel调整成下一层残差结构所需要的channel）

需要注意的是，对于ResNet50/101/152，其实conv2_x所对应的一系列残差结构的第一层也是虚线残差结构，因为它需要调整输入特征矩阵的channel。根据表格可知通过3x3的max pool之后输出的特征矩阵shape应该是[56, 56, 64]，但conv2_x所对应的一系列残差结构中的实线残差结构它们期望的输入特征矩阵shape是[56, 56, 256]（因为这样才能保证输入输出特征矩阵shape相同，才能将捷径分支的输出与主分支的输出进行相加）。所以第一层残差结构需要将shape从[56, 56, 64] --> [56, 56, 256]。注意，这里只调整channel维度，高和宽不变（而conv3_x, conv4_x, conv5_x所对应的一系列残差结构的第一层虚线残差结构不仅要调整channel还要将高和宽缩减为原来的一半）。

下面是 ResNet 18/34 和 ResNet 50/101/152 具体的实线/虚线残差结构图：

ResNet 18/34

ResNet 50/101/152

Batch Normalization

Batch Normalization是指批标准化处理，将一批数据的feature map满足均值为0，方差为1的分布规律。

Batch Normalization原理

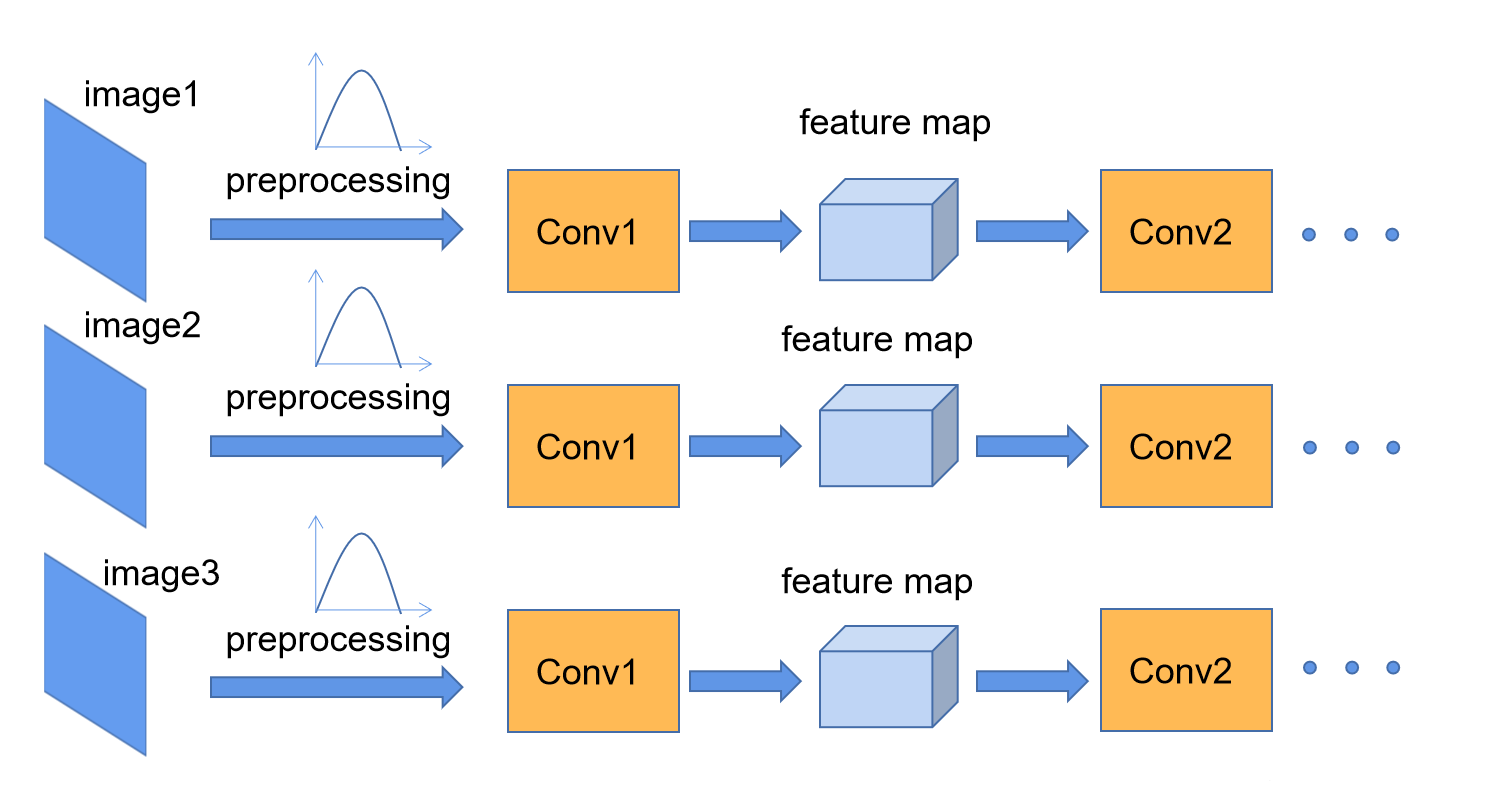
我们在图像预处理过程中通常会对图像进行标准化处理，这样能够加速网络的收敛，如下图所示，对于Conv1来说输入的就是满足某一分布的特征矩阵，但对于Conv2而言输入的feature map就不一定满足某一分布规律了（注意这里所说满足某一分布规律并不是指某一个feature map的数据要满足分布规律，理论上是指整个训练样本集所对应feature map的数据要满足分布规律）。

而我们Batch Normalization的目的就是使我们的feature map满足均值为0，方差为1的分布规律。

论文中的一段话：“对于一个拥有d维的输入x，我们将对它的每一个维度进行标准化处理。” 假设我们输入的x是RGB三通道的彩色图像，那么这里的d就是输入图像的channels即$d=3，x=(x^{(1)}, x^{(2)}, x^{(3)})$，其中$x^{(1)}$就代表我们的R通道所对应的特征矩阵，依此类推。标准化处理也就是分别对我们的R通道，G通道，B通道进行处理。

原文中的计算公式：

计算一个Batch数据的feature map然后在进行标准化（batch越大越接近整个数据集的分布，效果越好）。我们根据上图的公式可以知道代表着我们计算的feature map每个维度（channel）的均值。

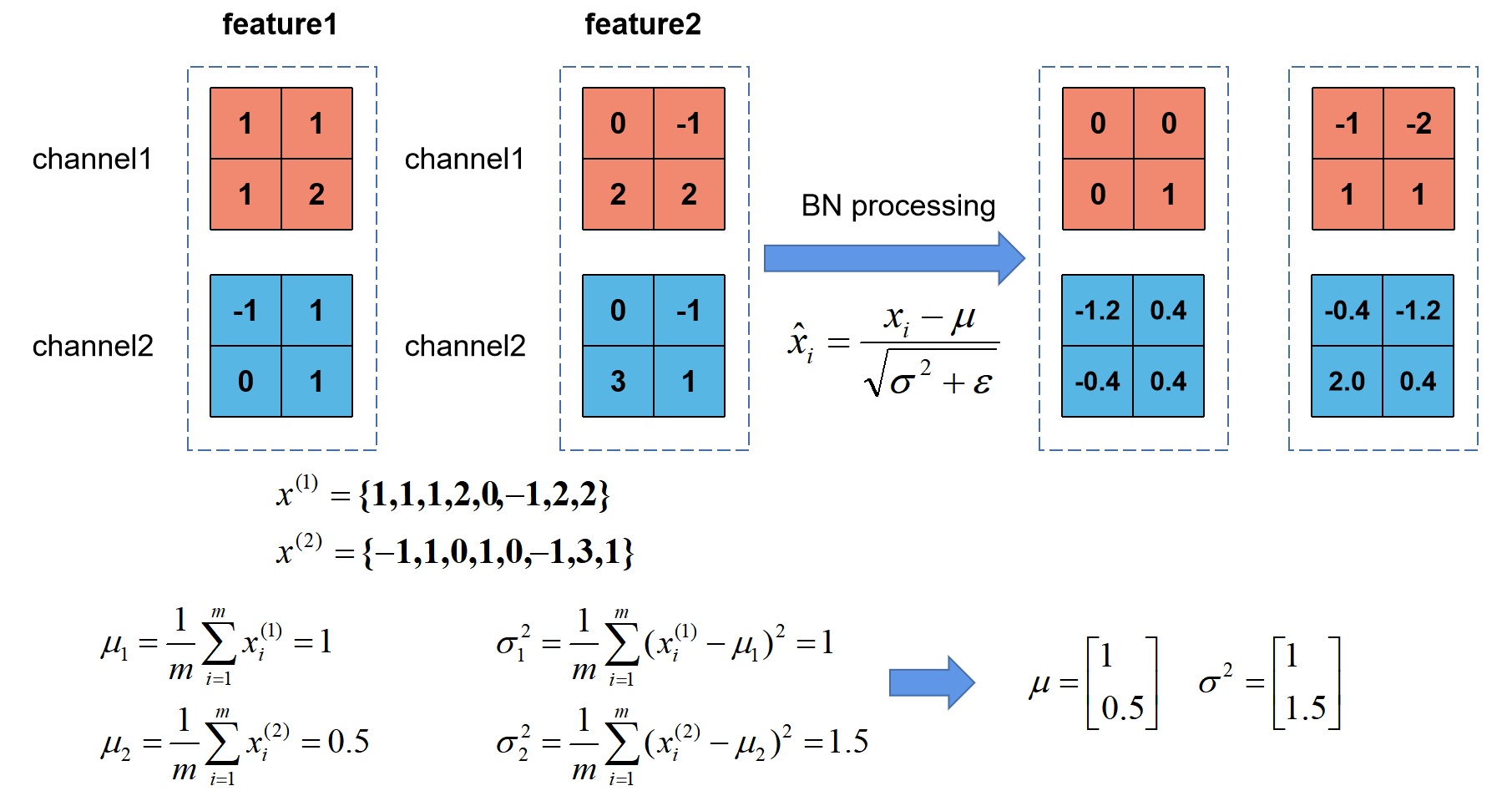
上图展示了一个batch size为2（两张图片）的Batch Normalization的计算过程，假设feature1、feature2分别是由image1、image2经过一系列卷积池化后得到的特征矩阵，feature的channel为2，那么代表该batch的所有feature的channel1的数据，同理代表该batch的所有feature的channel2的数据。

然后分别计算和的均值与方差，得到我们的和两个向量。然后在根据标准差计算公式分别计算每个channel的值（公式中的是一个很小的常量，防止分母为零的情况）。

在我们训练网络的过程中，我们是通过一个batch一个batch的数据进行训练的，但是我们在预测过程中通常都是输入一张图片进行预测，此时batch size为1，如果在通过上述方法计算均值和方差就没有意义了。

所以我们在训练过程中要去不断的计算每个batch的均值和方差，并使用移动平均(moving average)的方法记录统计的均值和方差，在训练完后我们可以近似认为所统计的均值和方差就等于整个训练集的均值和方差。

然后在我们验证以及预测过程中，就使用统计得到的均值和方差进行标准化处理。

γ，β是用来调整数值分布的方差大小，是用来调节数值均值的位置。这两个参数是在反向传播过程中学习得到的，γ的默认值是1，β的默认值是0。