1. 理解生成对抗网络
1.1 什么是生成对抗网络
1.1.1 大白话版
知乎上有一个很不错的解释,大家应该都能理解:
假设一个城市治安混乱,很快,这个城市里就会出现无数的小偷。在这些小偷中,有的可能是盗窃高手,有的可能毫无技术可言。假如这个城市开始整饬其治安,突然开展一场打击犯罪的「运动」,警察们开始恢复城市中的巡逻,很快,一批「学艺不精」的小偷就被捉住了。之所以捉住的是那些没有技术含量的小偷,是因为警察们的技术也不行了,在捉住一批低端小偷后,城市的治安水平变得怎样倒还不好说,但很明显,城市里小偷们的平均水平已经大大提高了。
警察们开始继续训练自己的破案技术,开始抓住那些越来越狡猾的小偷。随着这些职业惯犯们的落网,警察们也练就了特别的本事,他们能很快能从一群人中发现可疑人员,于是上前盘查,并最终逮捕嫌犯;小偷们的日子也不好过了,因为警察们的水平大大提高,如果还想以前那样表现得鬼鬼祟祟,那么很快就会被警察捉住。
为了避免被捕,小偷们努力表现得不那么「可疑」,而魔高一尺、道高一丈,警察也在不断提高自己的水平,争取将小偷和无辜的普通群众区分开。随着警察和小偷之间的这种「交流」与「切磋」,小偷们都变得非常谨慎,他们有着极高的偷窃技巧,表现得跟普通群众一模一样,而警察们都练就了「火眼金睛」,一旦发现可疑人员,就能马上发现并及时控制——最终,我们同时得到了最强的小偷和最强的警察。
1.1.2 非大白话版本
生成对抗网络(GAN)由2个重要的部分构成:
- 生成器(Generator):通过机器生成数据(大部分情况下是图像),目的是“骗过”判别器
- 判别器(Discriminator):判断这张图像是真实的还是机器生成的,目的是找出生成器做的“假数据”
下面详细介绍一下过程:
第一阶段:固定「判别器D」,训练「生成器G」
我们使用一个还 OK 判别器,让一个「生成器G」不断生成“假数据”,然后给这个「判别器D」去判断。
一开始,「生成器G」还很弱,所以很容易被揪出来。
但是随着不断的训练,「生成器G」技能不断提升,最终骗过了「判别器D」。
到了这个时候,「判别器D」基本属于瞎猜的状态,判断是否为假数据的概率为50%。
第二阶段:固定「生成器G」,训练「判别器D」
当通过了第一阶段,继续训练「生成器G」就没有意义了。这个时候我们固定「生成器G」,然后开始训练「判别器D」。
「判别器D」通过不断训练,提高了自己的鉴别能力,最终他可以准确的判断出所有的假图片。
到了这个时候,「生成器G」已经无法骗过「判别器D」。
循环阶段一和阶段二
通过不断的循环,「生成器G」和「判别器D」的能力都越来越强。
最终我们得到了一个效果非常好的「生成器G」,我们就可以用它来生成我们想要的图片了。
1.2 GAN的优缺点
3个优势
- 能更好建模数据分布(图像更锐利、清晰)
- 理论上,GANs 能训练任何一种生成器网络。其他的框架需要生成器网络有一些特定的函数形式,比如输出层是高斯的。
- 无需利用马尔科夫链反复采样,无需在学习过程中进行推断,没有复杂的变分下界,避开近似计算棘手的概率的难题。
2个缺陷
- 难训练,不稳定。生成器和判别器之间需要很好的同步,但是在实际训练中很容易D收敛,G发散。D/G 的训练需要精心的设计。
- 模式缺失(Mode Collapse)问题。GANs的学习过程可能出现模式缺失,生成器开始退化,总是生成同样的样本点,无法继续学习。
1.3 生成模型
1.3.1 生成模型简介
- 什么是生成模型
生成模型是指能够在给定某些隐含参数的条件下随机生成观测数据的模型,它给观测值和标注数据序列指定一个联合概率分布。在机器学习中,生成模型可以用来直接对数据建模,例如根据某个变量的概率密度函数进行数据采样,也可以用来建立变量间的条件概率分布,条件概率分布可以由生成模型根据贝叶斯定理形成。

对于生成模型来说,可以分为两个类型
- 第一种类型的生成模型可以完全表示出数据确切的分布函数
- 第二种类型的生成模型只能做到新数据的生成,而数据分布函数则是模糊的
我们讨论的生成对抗网络是第二种,第二种类型生成新数据的功能也通常是大部分生成模型的主要核心目标。
- 生成模型的作用
- 生成模型具备了表现和处理高维度概率分布的能力,而这种能力可以有效运用在数学或工程领域
- 生成模型,尤其是生成对抗网络可以与强化学习领域相结合,形成更多有趣的研究
- 生成模型亦可通过提供生成数据来优化半监督式学习
- 将生成模型用于超高解析度成像,可以将低分辨率的照片还原成高分辨率
1.3.2 自动编码器
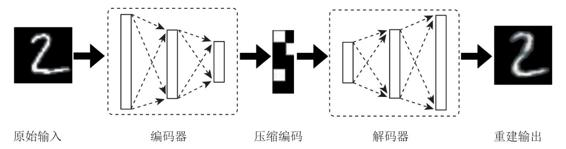
自动编码器是一种神经网络模型,该模型的最初意义是为了能够对数据进行压缩。
如图所示是一个标准的自动编码器,它的基本结构是一个多层感知器的神经网络,从输入层到输出层之间有多个隐含层,它的结构特点在于输入层与输出层拥有相同的节点数量,中间编码层的节点数量需要小于输入层与输出层的节点数。
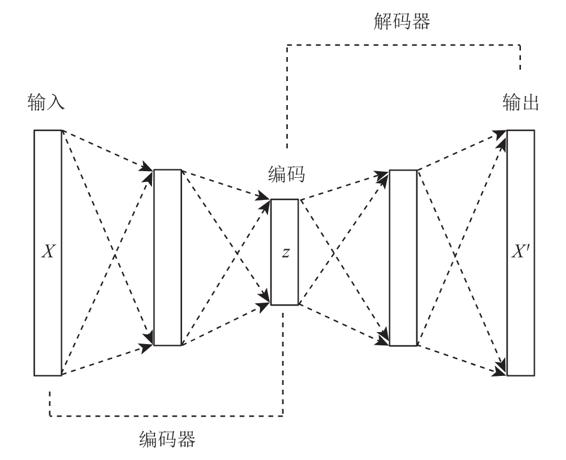
该网络结构希望能够在输出层产生的数据X′良好地还原出输入层的数据X,由于中间的编码层数据z拥有的维度数量低于输入层与输出层的维度,所以如果输出层可以还原输入层,相当于对输入数据进行了降维,也就是前面所说的数据压缩。
在自动编码器中,我们把输入层到编码层的网络部分(也就是整个神经网络的前半部分)称为编码器,把编码层到输出层的网络部分(后半部分)称为解码器。
编码器可以实现数据的压缩,将高维度数据压缩成低维度数据,解码器则可以将压缩数据还原成原始数据,当然由于对数据进行了降维处理,所以在还原的过程中数据会有一些损失。
自动编码器的训练过程需要将编码器与解码器绑定在一起进行训练,训练数据一般是无标签数据,因为我们会把数据本身作为它自身的标签。
1.3.3 变分⾃动编码器 (Variational Auto-Encoder,VAE)
相比于普通的自动编码器,变分自动编码器(VAE)其实才算得上是真正的生成模型。
为了解决自动编码器存在的不能通过新编码生成数据的问题,VAE在普通的自动编码器上加入了一些限制,要求产生的隐含向量能够遵循高斯分布,这个限制帮助自动编码器真正读懂训练数据的潜在规律,让自动编码器能够学习到输入数据的隐含变量模型。
如果说普通自动编码器通过训练数据学习到的是某个确定的函数的话,那么VAE希望能够基于训练数据学习到参数的概率分布。
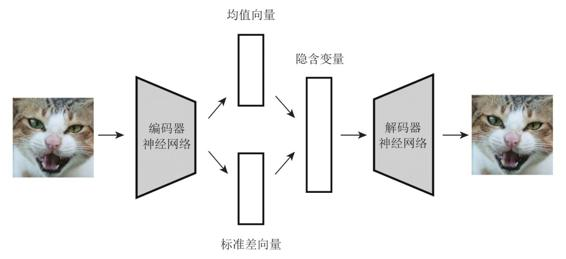
VAE具体的实现方法,在编码阶段我们将编码器输出的结果从一个变成两个,两个向量分别对应均值向量和标准差向量。通过均值向量和标准差向量可以形成一个隐含变量模型,而隐含编码向量正是通过对于这个概率模型随机采样获得的。最终我们通过解码器将采样获得的隐含编码向量还原成原始图片。
在实际的训练过程中,我们需要权衡两个问题
- 第一个是网络整体的准确程度
- 第二个是隐含变量是否可以很好地吻合高斯分布
对应这两个问题也就形成了两个损失函数:
- 第一个是描述网络还原程度的损失函数,具体的方法是求输出数据与输入数据之间的均方距离
- 第二个是隐含变量与高斯分布相近程度的损失函数
在这里我们需要介绍一个概念,叫作KL散度(Kullback–Leibler divergence),也可以称作相对熵。
KL散度的理论意义在于度量两个概率分布之间的差异程度:
- 当KL散度越高的时候,说明两者的差异程度越大
- 当KL散度低的时候,则说明两者的差异程度越小
- 如果两者相同的话,则该KL散度应该为0
采用KL散度来计算隐含变量与高斯分布的接近程度。
VAE的缺点:
训练过程中最终模型的目的是使得输出数据与输入数据的均方误差最小化,这使得VAE其实本质上并非学会了如何生成数据,而是更倾向于生成与真实数据更为接近的数据,甚至于为了让数据越接近越好,模型基本会复制真实数据。
1.4 GAN 可视化理解
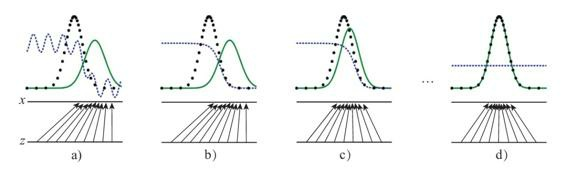
用一个可视化概率分布的例子来更深入地认识一下GAN。
点线为真实数据分布,实线为生成数据样本,在这个例子中的目标在于,让实线(也就是生成数据的分布)逐渐逼近点线(代表的真实数据分布)。
虚线为GAN中的判别器,在实验中我们赋予了它初步区分真实数据与生成数据的能力,并对于它的划分性能加上一定的白噪音,使得模拟环境更为真实。
输入域为z(图中下方的直线),在这个例子里默认为一个均匀分布的数据,生成域为x(图中上方的直线)为不均匀分布数据,通过生成函数$x=G(z)$形成一个映射关系,正如图中的那些箭头所示,将均匀分布的数据映射成非均匀数据。G在图中表示为两条水平直线间的箭头。
a到d展示了GAN的工作过程。a为初始状态,此时生成数据和真实数据有比较大的差距,判别器具备初步划分是否为真实数据的能力,但由于存在噪声,效果仍有缺陷。
b中通过使用标签对判别器训练,判别器开始向一个较完善的方向收敛,最后呈现图中的效果,此时:
$$ D^*(z)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)} $$
判别器完美后我们开始迭代生成器G,如c所示。通过判别器D的倒数梯度方向作为指导,我们让生成数据向真实数据的分布方向移动,让生成数据更容易被判别器判断为真实数据。
最后,判别器和生成器会进入d的状态,此时 $p_g$ 非常逼近甚至完全等于 $p_{data}$ ,当达到 $p_{data}=p_g$ 时,G生成的数据能够达到我们的预期,并能模拟出真实的数据分布;而D在这个状态下已经无法分辨两种数据分布,此时 $D(x)=\frac{1}{2}$ 。
1.5 GAN的工程实践
数学推导中我们知道,我们要做的是优化下面的式子。
$$ V= E_{x\sim P_{data}}log D(x)+E_{x\sim P_z}log(1-D(G(z)))\tag{1-1} $$
计算公式中的期望值可以等价于计算真实数据分布与生成数据分布的积分,在实践中我们使用采样的方法来逼近期望值。
首先我们从前置的随机分布$p_g(z)$中取出m个随机数$\{z^{(1)}, z^{(2)},…, z^{(m)}\}$,其次我们再从真实数据分布$$p_{data}(x)$$中取出m个真实样本$$\{x^{(1)} ,x^{(2)},...,x^{(m)} \}$$。我们使用平均数代替式(1-1)中的期望,公式改写如下。
$$ V=\frac{1}{m}\sum^m_{i=1}[log D(x^{(i)})+log(1-D(G(z^{(i)})))]\tag{1-2} $$
在GAN的原始论文中给出了完整的伪代码(见伪代码1-1),其中$\theta _d$为判别器D的参数,$\theta_g$为生成器G的参数。
伪代码1-1$$ \begin{array}{l} for \; 训练的迭代次数 \;do\\ \quad for \;重复k次 \;do\\ \qquad从生成器前置随机分布p_g(z)取出m个小批次样本z^{(1)},z^{(2)},...,z^{(m)};\\ \qquad从真实数据分布p_{data}(x)取出m个小批次样本x^{(1)},x^{(2)},...,x^{(m)};\\ \qquad使用随机梯度下降更新判别器参数;\\ \qquad\qquad \nabla_{\theta,d}\frac{1}{m}\sum^m_{i=1}[logD(x^{(i)})+log(1-D(G(z^{(i)})))]\\ \quad end\;for\\ \quad 从生成器前置随机分布p_g(z)取出m个小批次样本z^{(1)},z^{(2)},...,z^{(m)};\\ \quad 使用随机梯度下降更新生成器参数;\\ \qquad \nabla_\theta\frac{1}{m}\sum^m_{i=1}log(1-D(G(z^{(i)})))\\ end \;for \end{array} $$
该伪代码每次迭代过程中的前半部分为训练判别器的过程,后半部分为训练生成器。
对于判别器,我们会训练k次来更新参数$\theta_d$,在论文的实验中研究者把k设为1,使得实验成本最小。
生成器每次迭代中仅更新一次,如果更新多次,可能无法使得生成数据分布与真实数据分布的JS散度距离下降。
使用pytorch进行演示:
# 载入包
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(1) # 设置CPU的的随机数固定,使得紧跟着的rand() 函数生成的值是固定的随机
np.random.seed(1) # 先定义一个随机数种子
# 超参数设置
BATCH_SIZE = 64
LR_G = 0.0001 # 生成器学习率
LR_D = 0.0001 # 判别器学习率
N_IDEAS = 5 # 生成器G的学习灵感
ART_COMPONENTS = 15 # 生成器G创作的点数
# 一次处理中所产生的点数,二维矩阵
PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)]) # shape(64,15)
# 看看图
plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
plt.legend(loc='upper right')
plt.show()
# 定义绘图函数 G和D:
def artist_works(): # 著名艺术家的绘画(真正的目标)
a = np.random.uniform(1, 2, size=BATCH_SIZE)[:, np.newaxis]
#从[1,2)的正态分布中随机选取64个数字,并在第二维度新加一个维度
paintings = a * np.power(PAINT_POINTS, 2) + (a-1) # shape(64,15)
#生成这些点的纵坐标
paintings = torch.from_numpy(paintings).float()
# 将其转变为tensor数据
return paintings
G = nn.Sequential( # Generator 生成器
# G 将自己的灵感变成15个点
nn.Linear(N_IDEAS, 128), # 随机想法(可能来自正态分布)
nn.ReLU(),
nn.Linear(128, ART_COMPONENTS), # 用这些随意的想法画一幅画
)
D = nn.Sequential( # Discriminator 判别器
# 对画作进行鉴别,输出一个它判断该画作是否为著名画家画作的概率值,sigmoid()用于生成一个概率值
nn.Linear(ART_COMPONENTS, 128), # 接受著名艺术家或像G这样的新手的艺术作品
nn.ReLU(),
nn.Linear(128, 1),
nn.Sigmoid(), # 告诉艺术家创作艺术品的可能性
)
# 当在class中才需要新建实例
opt_D = torch.optim.Adam(D.parameters(), lr=LR_D)
opt_G = torch.optim.Adam(G.parameters(), lr=LR_G)
# 训练
epochs=10000 # 训练次数
for step in range(epochs):
artist_paintings = artist_works()
# 著名画家的画作
G_ideas = torch.randn(BATCH_SIZE, N_IDEAS, requires_grad=True) # shape(64,5)
# 用于随机生成generator的灵感
G_paintings = G(G_ideas)
# 根据生成的灵感来作画
prob_artist1 = D(G_paintings) # D try to reduce this prob
# discriminator判断这些画作(G自己的灵感画作)来自著名画家的概率为多少
G_loss = torch.mean(torch.log(1. - prob_artist1))
#这种概率要越低越好,因为它是永远是在模仿
#优化
opt_G.zero_grad() # 将模型中的梯度清零
G_loss.backward() # 求目标函数的梯度
opt_G.step() # 梯度下降,更新G的参数
prob_artist0 = D(artist_paintings)
# discriminator判断这些画作(著名画家画作)来自著名画家的概率为多少,希望越高越好
prob_artist1 = D(G_paintings.detach()) #锁住G的参数不求导
#G_paintings的梯度不会更新
D_loss = - torch.mean(torch.log(prob_artist0) + torch.log(1. - prob_artist1))
# 我们是希望它越大越好,但是torch中只有减小误差才会提升
opt_D.zero_grad()
D_loss.backward(retain_graph=True)
# retain_graph是为了再次使用计算图纸
opt_D.step()
if step % 1000 == 0: # plotting
plt.cla()
plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0], c='#4AD631', lw=3, label='Generated painting',)
plt.plot(PAINT_POINTS[0], 2 * np.power(PAINT_POINTS[0], 2) + 1, c='#74BCFF', lw=3, label='upper bound')
plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0, c='#FF9359', lw=3, label='lower bound')
plt.text(-.5, 2.3, 'D accuracy=%.2f (0.5 for D to converge)' % prob_artist0.data.numpy().mean(), fontdict={'size': 15})
plt.text(-.5, 2, 'D score= %.2f (-1.38 for G to converge)' % -D_loss.data.numpy(), fontdict={'size': 15})
plt.ylim((0, 3))
plt.legend(loc='upper right', fontsize=12)
plt.draw()
plt.pause(0.01)
plt.show()
在这个GAN例子中,需要注意的点有:
PAINT_POINTS = np.vstack([np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)])
为什么不直接写PAINT_POINTS = [np.linspace(-1, 1, ART_COMPONENTS) for _ in range(BATCH_SIZE)],而是非要再加上一个np.vsatck()来进行过垂直合并?

到这里,应该可以看出差别了,如果直接用[]list生成的话,它俩是不兼容的,因为用np.linspace()生成的是numpy数据,而使用np.vstack()之后,它俩就都变成numpy可以进行运算了。
- 另一个比较迷惑的点是:下面两个loss究竟代表什么
D_loss = -torch.mean(torch.log(prob_a)+torch.log(1.-prob_artist1))在gan中我们希望torch.mean(torch.log(prob_a)+torch.log(1.-prob_G))是越大越好,而神经网络中差值越小才有利于神经网络的提升,所以要加一个负号。
G_loss = torch.mean(torch.log(1.-prob_artist1))在gan中要G_loss越小越好,所以用1.-prob_G
对应真正的图片打分高,也就是最大化如下公式,公式如下:
$$ \frac{1}{m}\sum^m_{i=1}log D(x^i) $$
对于生成出来的图片,希望对它的打分尽可能低,由公式中的第二部分可以解释
$\frac{1}{m}\sum^m_{i=1}(1-log D(\tilde{x}^i))$,原公式是最大化它,等价于最小化$\frac{1}{m}\sum^m_{i=1}(logD(\tilde{m}^i))$
(公式太多了 还是得再看看)